論理演算の基本系を勉強します。
勉強のきっかけになった過去問
論理式P,Qがいずれも真であるとき,論理式Rの真偽にかかわらず真になる式はどれか。ここで," ̄"は否定,"∨"は論理和,"∧"は論理積,"→"は含意("真→偽"となるときに限り偽となる演算)を表す。
基本編
論理和は「OR」です。
論理積は「AND」です。
否定は「NOT」です。
否定は「1」なら「0」になります。
| A | NOT |
| 1 | 0 |
| 0 | 1 |
- 否定の論理回路はこれです。
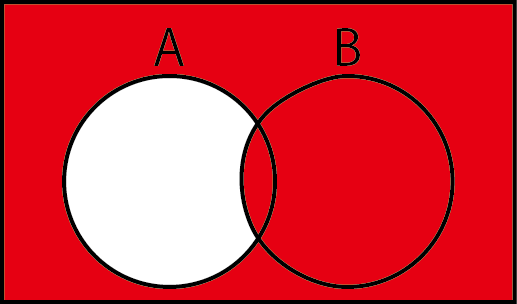
- ベン図はこうなります。
- 否定は
 で表されます。
で表されます。
- キーボードで何を打てば出るかわかりませんでした。「¬」も否定の記号です。「ひてい」とうって変換したら出ました。
含意は「AならばB」ということらしいです。
「ふくい」ではなく「がんい」とよみます。
kotobank.jp
言葉遊びのようで日本語が弱いためよくわかりません。
含意の命題「ならば」をあらわす論理記号 A⇒B [数学についてのwebノート]
他の方法で考えます。
英語でわかるわけがありません。
connotation、entailment、implication、implicature、intent、connote、imply、imply、stand for、signify、intend、meanなどなど
記号はわかりません。
「A→B」「A⇒B」「A⊃B」
※. 正しくは「A→B」と「A⇒B」は異なるらしいけれどそんなレベルにはいません。
論理包含 - Wikipedia
真理値表はよくわかりません。
| A | B | 含意 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
- 10進数にしても全くわかりません。
- A = 12 = 1100
- B = 5 = 0101
- A ⊃ B = 1011 = 11
ベン図は不思議に感じます。
解りにくければ、A≦B と覚えればOK!
softwaredevelop.web.fc2.com